Problem - Min & Max Sum of N-1 Elements Of Array

Problem

Coder Raco was playing with an integer array. The Array stores random integers, and the problem he wants to solve is to find the minimum and maximum sum of N-1 elements.

minimum sum is: 33 (2+5+7+9+10)
maximum sum is: 43 (5+7+9+10+12)

Another case:

Here, minmum sum is: 32 & maximum sum is: 46

Solution Approach

Hint

1. You can find the minimum and maximum numbers in the array and use that to calculate the sum.

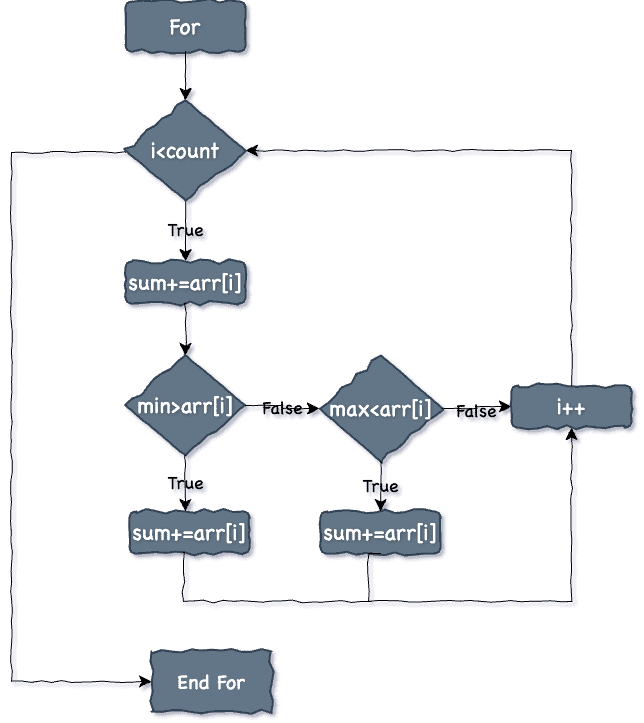
Algorithm

• Initialize a ‘sum’ variable with the value of zero to store the sum of elements of the array.
• Initialize a ‘min’ & ‘max’ variable to store the minimum & maximum number in the array.
• Assign the first element value as the default value to min & max.
• Start a for loop with the condition till i is less than the array length.
• Add element in sum.
• Assign element to min if it is less than min.
• Assign element to max if it is greater than max.
• Continue .

Code Examples (C)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

void minMaxSum(int *integerArray, int arrayCount) {
    long minNumber = 0;
    long maxNumber = 0;
    long sum = 0;
    if (arrayCount <= 0) {
        printf("Invalid input");
    }
    
    minNumber = integerArray[0];
    maxNumber = minNumber;
    
    for(int index = 0; index < arrayCount; index++) {
        sum += integerArray[index];
        
        if (integerArray[index] < minNumber) {
            minNumber = integerArray[index];
        } else if (integerArray[index] > maxNumber) {
            maxNumber = integerArray[index];
        }
    }
    
    long minSum = (sum - maxNumber);
    long maxSum = (sum - minNumber);
    
    printf("%lu %lu", minSum, maxSum);
}

Complexity

Time Complexity O(n)

Since the number of iterations is equal to length of array, the code’s time complexity is O(N).

Space Complexity O(1)

A constant space is required to store variables, so the space complexity is O(1).