Problem - Count Set Bits In An Integer

Problem

Help Coder Raco to count set digits in an Integer. He is designing a lift system. He utilises a bit within an integer to represent the floor number. Lift stops at a floor if a corresponding bit is set.

In the following example, the lift stops at floors 1 and 3.

Before designing the complete system, he wanted to solve a simple problem: count the number of bits set in a binary representation of an integer.

For example, in the above case, the output should be 2.

Some more examples:

Solution Approach

Brute Force

Raco has a naive approach that goes through all bits and verifies whether it is set or not. There are two operations here:

1. Run a Loop.
2. Verify bit.

But how to achieve these?

Hint

1. To go through all the bits of an integer, you can use the right shift operator »
2. To verify whether a bit is set, perform bitwise & with one.

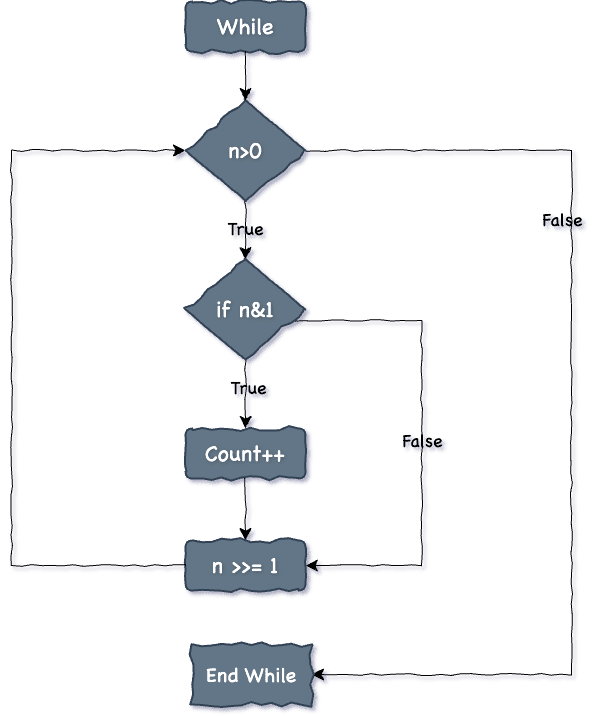
Algorithm

• Initialize a ‘count’ variable to store the count of the total set bits in the integer.
• Start a while loop with the condition till N is greater than zero. N here is the Integer used to store bits.
• Take Bitwise AND of the number ‘N’ with 1 to check if the rightmost bit is set
• Increment the ‘count’ if the bit is set.
• Shift the number to the right using the right shift operator.

Binary Number System

Here, Raco wants to apply logic based on how the binary number system works. The binary number system has a base of 2 in which numbers are represented only by two digits, 0 and 1. You divide the number by two until the quotient is zero, and reminders in the process are your binary representation. Binary numbers power of two have a pattern.

Hint

1. you can use powers of two in a loop to verify a number (power value = position of bit).

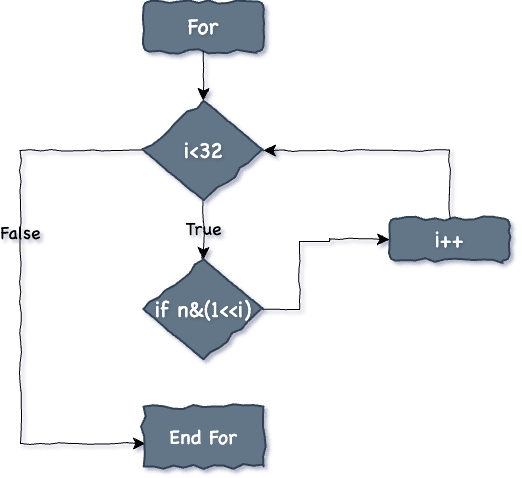
Algorithm

• Initialize a ‘count’ variable to store the count of the total set bits in the integer.
• Start a for loop with the condition till i is less than 32/64. 32 or 64 here is the size of Integer 32-bit or 64-bit.
• Take Bitwise AND of the number ‘N’ with (1«i). Here, (1«i) is same as pow(2, i).
• Increment the ‘count’ if the result is true.

Code Examples (C)

Brute Force

int setCountBit(int number) {
    // Initialising a variable to count the 0.
    int count = 0;
    while (number){
        // If the last bit is 1, increment the count
        if((number&1)>0){
            ++count;
        }
        // Right shift the value of number
        number >>= 1;
    }
    return count;
}

Complexity

Time Complexity O(log(N))

Since a number has maximum log(N) set bits, and we are going through all the bits one by one, this approach’s time complexity is O(log(N)).

Space Complexity O(1)

A constant space is required to store a variable, so the space complexity is O(1).

Binary Number System Approach

int setCountBitPowerMethod(int number) {
    // Initialising a variable count to 0.
      int count = 0;
      // Iterating over all the bits. Considering Int size 32 bit
      for(int bitIndex = 0 ; bitIndex < 32 ; bitIndex++){
          if(number & (1<<bitIndex)){
              ++count;
          }
      }
      return count;
}

Complexity

Time Complexity O(1)

Since the number of iterations is fixed at 32, regardless of the input size, the code’s time complexity is O(1).

Space Complexity O(1)

A constant space is required to store a variable, so the space complexity is O(1).

Bonus Solution (Brian Kernighan’s Algorithm)

An interesting solution for the problem is Brian Kernighan’s Algorithm. According to the algorithm the Bitwise AND of 2 numbers, i.e., N & (N - 1), unsets the rightmost set bit of the original number N.

So, we start a while loop to do N & (N - 1) to unset the rightmost set bit of the integer in every iteration. One thing to keep in mind is that the number of times the loop executes equals the number of set bits in that integer. For example, for the integer value 7, the loop will run 3 times so the set bit count is 3.